Electron has two invisible companions
- Spin: an intrinsic form of angular momentum, not because it literally spins, but because it behaves as if it does.
- Magnetic moment: the magnetic “strength” and direction associated with that spin.
Magnetic moment in a static magnetic field
When an object possessing a magnetic moment is placed in a magnetic field B0 it experiences a torque. which causes the spin S to wobble around the direction of B0 with an angular frequency as shown in Fig. 1.
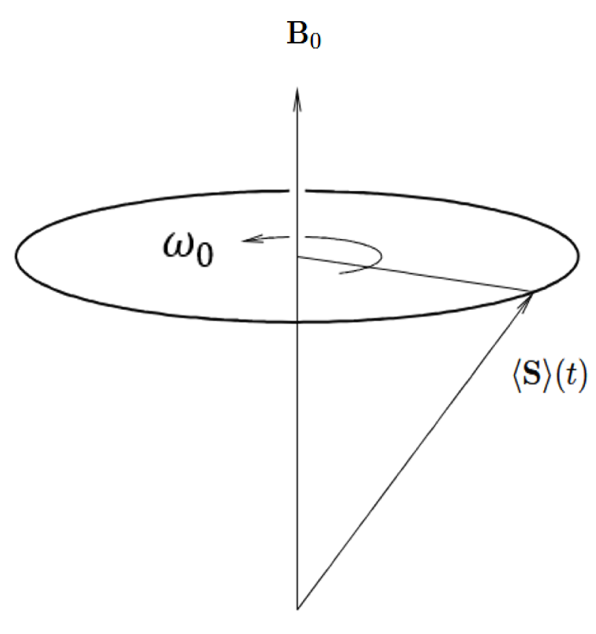
This phenomenon is called as precession and its frequency depends solely on the magnitude of the staic magnetic field.
Note: The angle between S to B0 depends on the initial spin orientation and due to environmental effects it relaxes slowly to the direction of B0. We are not discussing about it at all as the precession happens irrespective that angle.
Ingredient to topple the spin
For changing the spin direction, It is obvious to consider using an additional static magnetic field B1 perpendicular to B0, to put a torque on the magnetic moment. At first, this idea seems somewhat convincing. However, due to the ongoing spin precession, the angle between the spin vector and any applied constant field will keep changing. This causes unpredictability of the behaviour.
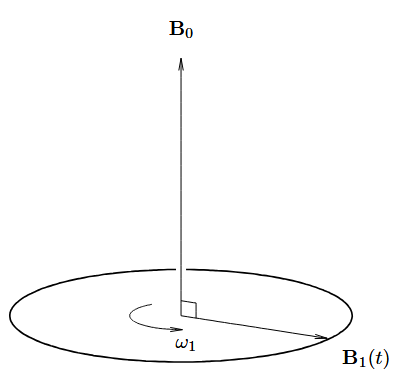
We can think of a way out of this by somehow applying a rotating magnetic field B1(t) in the plane perpendicular to B0. This method helps us try to keep the direction of torque always away from the direction of B0. This is illustrated in Fig. 2.
Plan in action
Let’s assume that we have applied the B1(t) in the configuration mentioned in Fig. 1. It is easy to think that fully utilizing the toppling strength of B1 requires precise rotation. It should match the frequency of precession due to B0. This is to keep the torque always away from the direction of B0.
However, in general, they are not equal. Which will make the behavior of the spin quite complicated. To simplify the understanding, we will change our frame of reference to the rotating frame of B1. In this frame, B1 will not be seen as changing its direction. It will behave as a static field. We can call it B10.
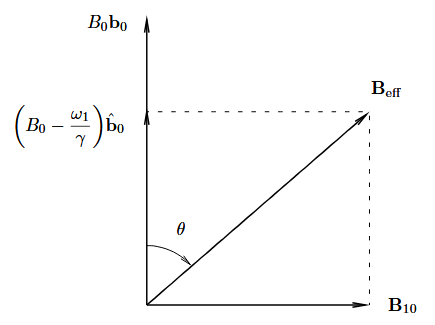
It might seem, at first glance, that the net magnetic field in the rotating frame is the vector sum of B0 and B10. However, we completely ignored one crucial fact. The precession will appear to have less frequency since we ourselves are rotating. The apparent precession rate would be :
This suggests that the apparent magnetic field will be lesser than B0. As stated by equations below and the Fig. 3(a).
.
The effective magnetic field Beff will cause the spin to precess around its own direction with an angular frequency .
In the lab frame the spin S will precess about the direction of Beff lets call it . This axis
, will itself precess about B0 as shown in Fig. 4.
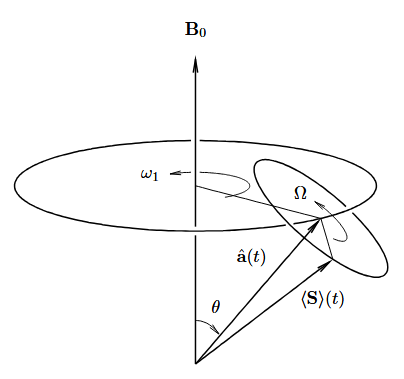
From the Fig. 3, The angle can be expressed as:
One interesting thing to observe here would be the case which we guessed at the beginning, . With this situation the
will become 900.
This means that the spin will now sweep a cone around an axis in the plane perpendicular to B0 having
.
If we assume that the initial spin was fully aligned with B0 (Making precession without having any angle with B0), this cone will become a circle with having rotating axis, always perpendicular to B0. And now we can see that the spin is changing its direction all the way from +z to -z if we consider that B0 is aligned in z direction. This switching will happen at the rate of . which is also called as Rabi Flopping Frequency. At resonance it can be defined as:
As a conclusion we have understood that spin flipping works best at which is the condition of maximum energy transfer and is also known as Electron Spin Resonance.
Rotating magnetic field? How to produce it?
We have understood ESR in an easy way. But the assumption of having a rotating magnetic field seems impractical. However, we can instead apply an oscillating magnetic field:
Assuming is perpendicular to z direction.
can be further broken into two components:
The first term with addition can be called as co-rotating term and the second is counter rotating.
The co-rotating term will appear to be static in the rotating frame. The counter rotating term will appear to have a doubled angular frequency. This in rotating field approximation will cause very small change and can be ignored. The Co-rotating term behaves exactly as the fictitious rotating magnetic field we needed for ESR.